PROCESOS ESTOCÁSTICOS EN TIEMPO DISCRETO
Grado en Estadística- Plan 2016
Curso 2017/2018
1. Datos de la asignatura
(Fecha última modificación: 20-06-18 12:53)- Código
- 108414
- Plan
- 2016
- ECTS
- 6.00
- Carácter
- OBLIGATORIA
- Curso
- 2
- Periodicidad
- Segundo Semestre
- Idioma
- ESPAÑOL
- Área
- ESTADÍSTICA E INVESTIGACIÓN OPERATIVA
- Departamento
- -
- Plataforma Virtual
Datos del profesorado
- Profesor/Profesora
- María Jesús Rivas López
- Grupo/s
- 1
- Centro
- Fac. Ciencias
- Departamento
- Estadística
- Área
- Estadística e Investigación Operativa
- Despacho
- Edif. Ciencias D1509
- Horario de tutorías
- -
- URL Web
- -
- chusrl@usal.es
- Teléfono
- 670620488
2. Sentido de la materia en el plan de estudios
Bloque formativo al que pertenece la materia.
Probabilidad
Papel de la asignatura.
Dar continuidad a la iniciación a la Probabilidad que se estudia en las asignaturas “Introducción a la Probabilidad” y “Cálculo de Probabilidades” de primer y segundo curso, que pueda servir de soporte y herramienta para asignaturas de los demás módulos.
Perfil profesional.
Profesiones relacionadas con las ciencias de la salud, economía e industria.
3. Recomendaciones previas
Las generales para acceder al Grado de Estadística y haber cursado las asignaturas “Introducción a la Probabilidad” y “Cálculo de Probabilidades”.
4. Objetivo de la asignatura
GENERALES:
- Conocer la naturaleza, métodos de trabajo y fines de los procesos estocásticos.
- Reconocer la necesidad de los procesos estocásticos para abordar muchas situaciones reales en las que interviene el azar o exista incertidumbre.
- Desarrollar las capacidades analíticas y de abstracción, la intuición y el pensamiento lógico, riguroso y crítico a través del estudio de la Probabilidad.
- Capacitar para la utilización de los conocimientos teóricos y prácticos adquiridos en la definición y planteamiento de problemas y en la búsqueda de sus soluciones tanto en contextos académicos como profesionales.
- Preparar para posteriores estudios especializados que requieran fundamentos probabilísticos.
ESPECÍFICOS:
- Que el alumno conozca, comprenda y maneje las nociones básicas de las cadenas de Markov, de manera que sepa hallar sus distribuciones y resolver problemas reales mediante su uso.
- Comprender los conceptos relacionados con un problema de colas y manejar las situaciones modeladas por procesos de nacimiento y muerte o que sigan modelos de colas simples.
- Conocer las diferentes componentes de una serie temporal aplicando datos reales y saber hacer un estudio de su estacionalidad.
5. Contenidos
Teoría.
BLOQUE 1: CADENAS DE MARCOV.
TEMA 1: ELEMENTOS DE UNA CADENA DE MARCOV. Procesos estocásticos. Cadenas de Markov. Cadenas de Markov homogéneas. Distribuciones de una cadena de Markov.
TEMA 2: COMPORTAMIENTO DE UNA CADENA DE MARCOV. Clasificación de los estados de una cadena de Markov. Propiedades de los estados de una cadena de Markov. Distribuciones estacionarias. Distribuciones límite.
BLOQUE 2: TEORÍA DE COLAS.
TEMA 3: DESCRIPCIÓN DE UN PROBLEMA DE COLAS. Características de los sistemas de colas. Notación de Kendall. Medidas de eficiencia de un sistema de colas. Recogida de datos en un sistema de colas.
TEMA 4: LOS PROCESOS DE POISSON Y LA DISTRIBUCIÓN EXPONENCIAL. Distribuciones Exponencial y Erlang. Procesos de Poisson. Propiedades del patrón de llegadas Poisson-Exponencial. Procesos de nacimiento-muerte. Estabilidad.
TEMA 5: MODELOS DE COLAS SIMPLES. Estudio del sistema de colas M/M/1: Distribución estacionaria y Medidas de eficiencia. Colas con más de un canal de servicio: Sistema M/M/c. Colas con restricción en capacidad del sistema: Sistemas M/M/1/k y M/M/c/k.
BLOQUE 3: SERIES TEMPORALES.
TEMA 7: ANÁLISIS CLÁSICO DE SERIES TEMPORALES. Definición de serie temporal. Componentes. Criterios para detectar el modelo.
TEMA 8: DESCOMPOSICIÓN DE UNA SERIE TEMPORAL. Análisis de tendencia. Análisis de estacionalidad. Análisis del ciclo. Alisado de series temporales.
6. Competencias a adquirir
Específicas.
CE011.- Conocer los principales tipos de procesos estocásticos (con CB1, CG1, CE3).
CE021.- Aprender a modelar situaciones reales mediante procesos estocásticos (con CB2, CB3, CG5, CE2, CE3).
CE031.- Ser capaz de aplicar las técnicas estudiadas a procesos concretos (con CBCE3, CE2).
041.- Desarrollar un entendimiento profundo de las ideas probabilísticas (con CB1, CG5, CE5).
Transversales.
INSTRUMENTALES:
CT012.- Capacidad de análisis y síntesis.
CT022.- Capacidad de organización y planificación.
CT032.- Capacidad de gestión de la información.
CT042.- Resolución de problemas.
CT052.- Toma de decisiones a partir de los resultados obtenidos.
INTERPERSONALES:
CT062.- Trabajo en equipo.
CT072.- Razonamiento crítico.
CT082.- Compromiso ético.
CT092.- Habilidades en las relaciones interpersonales.
SISTÉMICAS:
CT102.- Aprendizaje autónomo.
CT112.- Motivación por la calidad del aprendizaje.
7. Metodologías
Se expondrá el contenido teórico de los temas a través de clases presenciales, siguiendo el texto recomendado para cada bloque, que servirá para fijar los conocimientos ligados a las competencias previstas y dar paso a clases prácticas de resolución de problemas, en los que se aplicarán las definiciones, propiedades y teoremas expuestos en las clases teóricas, de modo que en las clases prácticas los estudiantes se inicien en las competencias previstas.
A partir de las clases teóricas y prácticas se propondrá a los alumnos la realización de trabajos personales sobre problemas que aparecen en situaciones reales, para cuya realización tendrán el apoyo del profesor en seminarios tutelados. En esos seminarios los estudiantes podrán compartir con sus compañeros y con el profesor las dudas que encuentren, obtener solución a las mismas y comenzar a desempeñar por si mismos las competencias de la materia.
Además, los estudiantes tendrán que desarrollar por su parte un trabajo personal de estudio y asimilación de la teoría, resolución de problemas propuestos y preparación de los trabajos propuestos, para alcanzar las competencias previstas. De ello tendrán que responder, exponiendo sus trabajos ante el profesor y el resto de compañeros y comentándolos luego en una tutoría personal entre estudiante y profesor, así como realizando exámenes de teoría y resolución de problemas.
8. Previsión de Técnicas (Estrategias) Docentes
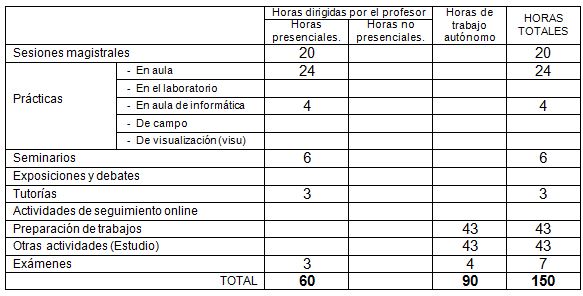
9. Recursos
Libros de consulta para el alumno.
VÉLEZ, R. e IBARROLA, P. (1977) Procesos Estocásticos. UNED.
RODRIGUEZ MORILLA, C. (2000). Análisis de series temporales. Cuadernos de Estadística. La Muralla-Hespérides.
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
QUESADA, V. y PARDO, L. (1987). Curso Superior de Probabilidades. PPU, Barcelona.
ROSS, S. M. (1989). Introduction to Probability Models. Academic Press.
PAZOS ARIAS, J.J. (2003). Teoría de colas y simulación de eventos discretos. Pearson Educación D.L.
PEÑA, D. (2005). Análisis de series temporales. Alianza Editorial.
URIEL, E. (2005). Introducción al análisis de series temporales. Paraninfo.
10. Evaluación
Consideraciones generales.
Será el resultado de una ponderación basada en el desarrollo de cuestiones y ejercicios planteados a los alumnos durante el curso, las exposiciones en clase, las prácticas y de la nota obtenida en un examen escrito de teoría y problemas, en el que habrá que sacar, al menos, 3 puntos sobre 10.
Criterios de evaluación.
Para los dos primeros bloques
Las cuestiones y ejercicios planteados a los alumnos durante el curso supondrán un 20% de la nota final. Las exposiciones en clase supondrán un 20% de la nota final.
La evaluación final será por medio de prueba escrita que supondrá un 60% de la nota final.
Para el último bloque
El 50% de la nota corresponderá a una práctica de ordenador desarrollada en el aula. El otro 50% de la nota será por medio de prueba escrita el día de la evaluación final.
Instrumentos de evaluación.
Pruebas escritas y prácticas con ordenador.
Recomendaciones para la evaluación.
Estudiar la asignatura de forma regular desde el principio.
Preparar la teoría simultáneamente con la realización de problemas.
Consultar a los profesores las dudas que se tengan.
Recomendaciones para la recuperación.
Preparar la teoría simultáneamente con la realización de problemas.
Consultar a los profesores las dudas que se tengan.


