MATEMÁTICAS II
GRADO EN INGENIERÍA ELECTRÓNICA INDUSTRIAL Y AUTOMÁTICA
Curso 2018/2019
1. Datos de la asignatura
(Fecha última modificación: 05-07-18 10:31)- Código
- 106401
- Plan
- 264
- ECTS
- 6.00
- Carácter
- BÁSICA
- Curso
- 1
- Periodicidad
- Segundo Semestre
- Idioma
- ESPAÑOL
- Área
- MATEMÁTICA APLICADA
- Departamento
- Matemática Aplicada
- Plataforma Virtual
Datos del profesorado
- Profesor/Profesora
- José Luis Hernández Pastora
- Grupo/s
- Todos
- Centro
- Fac. Ciencias
- Departamento
- Matemática Aplicada
- Área
- Matemática Aplicada
- Despacho
- Casa del Parque 2, despacho nº 1
- Horario de tutorías
- Martes de 9:30 h a 11:00 h y Jueves de 12:00 h a 13:00 h. Los viernes de 9:00 h a 14:00 h en Facultad de Ciencias (Salamanca).
- URL Web
- -
- jlhp@usal.es
- Teléfono
- Teléfono Ext. 1574
2. Sentido de la materia en el plan de estudios
Bloque formativo al que pertenece la materia.
Materias Básicas.
Papel de la asignatura.
Materia de formación básica que permita al alumno adquirir competencias y conocimientos matemáticos del Cálculo en una y varias variables.
Perfil profesional.
Ingeniero Industrial.
3. Recomendaciones previas
Los requisitos previos para el alumno son los que se indican en las pruebas de acceso a la Universidad.
4. Objetivo de la asignatura
El curso presenta una iniciación y profundización en el Cálculo, teniendo en cuenta que su conocimiento es absolutamente imprescindible en la formación de cualquier ingeniero.
De manera más concreta, los objetivos generales de la asignatura son:
- Modelizar situaciones que aparecen en los problemas de ingeniería y, en general, de las ciencias aplicadas.
- Utilizar las técnicas matemáticas exactas y aproximadas.
- Conseguir un dominio de las técnicas diferenciales e integrales en funciones de una variable.
- Introducción a las técnicas del Cálculo Diferencial y Cálculo Integral en varias variables.
- Sucesiones y series de números y funciones.
5. Contenidos
Teoría.
BLOQUE I.
1.-FUNCIONES REALES. LÍMITES Y CONTINUIDAD
Números complejos. Funciones reales de una variable. Límites y sus propiedades. Continuidad. Algunos teoremas para funciones continuas.
2.-CÁLCULO DIFERENCIAL EN UNA VARIABLE
Introducción. Derivada de una función en un punto. Función derivada. Derivadas sucesivas. Propiedades de las derivadas. La Regla de L’Hòpital. Extremos relativos de una función. El teorema del valor medio.
BLOQUE II.
1.-CÁLCULO INTEGRAL EN UNA VARIABLE
Introducción. Primitiva de una función. La integral definida. El teorema fundamental del cálculo. Integrales impropias.
2.-SUCESIONES Y SERIES
Sucesiones convergentes y divergentes. Límites de sucesiones. Series de números reales. Criterios de convergencia. Series de potencias.
3.- CÁLCULO EN VARIAS VARIABLES
Introducción al cálculo de funciones de varias variables.
6. Competencias a adquirir
Específicas.
CG3 - CG4 - CB1.
Transversales.
CT1- CT2 - CT3 - CT4 - CT5 - CT8 - CT9.
7. Metodologías
En esta asignatura planteamos y desarrollamos actividades presenciales y no presenciales.
Las actividades formativas presenciales se clasifican de la siguiente manera:
- Actividad de Grupo Grande: Exposición, explicación y ejemplificación de los contenidos. Lección magistral y resolución de ejercicios por el profesor.
- Actividad de Grupo Medio: Resolución de problemas y/o casos prácticos. Lección magistral y resolución de ejercicios por el profesor.
- Tutorías: Individual / Grupo. Seguimiento personalizado del aprendizaje del alumno.
- Realización de exámenes. Desarrollo de los instrumentos de evaluación
Entre las actividades no presenciales, hemos de detallar:
- Estudio personal de los contenidos teóricos y realización de los problemas.
- Preparación de los trabajos y elaboración de informes.
- Preparación de los exámenes.
8. Previsión de Técnicas (Estrategias) Docentes
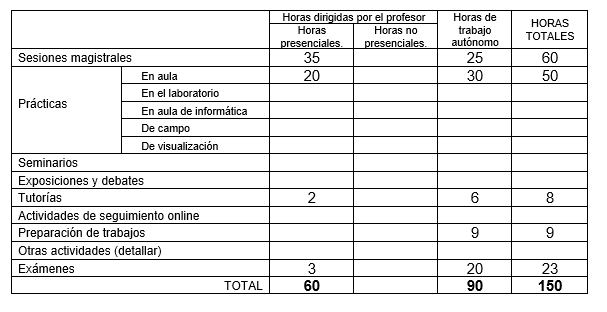
9. Recursos
Libros de consulta para el alumno.
- J. Burgos, Cálculo Infinitesimal de una variable. McGraw-Hill.
- T. de Bustos Muñoz. Teoría de Fundamentos II: Cálculo. Editorial Revide.
- J. Marsden. Cálculo Vectorial. Addison-Wesley.
- G. Rodríguez Sánchez. Cálculo I. Teoría y Problemas de Análisis Matemático en una variable. Editorial Clagsa.
- G. Rodríguez Sánchez. Cálculo II. Teoría y Problemas de funciones de varias variables. Editorial Clagsa.
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
La bibliografía y enlaces de Internet útiles se comentarán en detalle a lo largo del curso con otros contenidos de interés por su carácter clásico, novedoso, su aportación en las aplicaciones, etc.
10. Evaluación
Consideraciones generales.
El proceso de evaluación se llevará a cabo teniendo en cuenta el trabajo realizado por el alumno durante todo el semestre: elaboración de ejercicios, realización de exámenes y participación en las actividades docentes.
Criterios de evaluación.
La calificación final del curso se obtendrá teniendo en cuenta las distintas actividades propuestas:
La calificación final se obtendrá con la siguiente ponderación de las pruebas de evaluación:
1) Evaluación continua. Control en horario de clase: 20%
2) Examen final: 80%. La obtención de una calificación mínima de 4/10 es obligatoria para alcanzar la ponderación del resto de pruebas de evaluación y poder superar la asignatura.
Instrumentos de evaluación.
1) Control en horario de clase: Un examen de los contenidos del Bloque I al finalizar su desarrollo y otro de los contenidos del Bloque II al finalizar este.
2) Examen final: contenidos de ambos bloques docentes de la asignatura
Recomendaciones para la evaluación.
La resolución de ejercicios, trabajos y control se consideran indispensables y a su vez de gran ayuda para garantizar una comprensión adecuada de la asignatura y una evaluación positiva de la misma.
En la primera convocatoria se aplicarán todos los instrumentos de evaluación citados.
Recomendaciones para la recuperación.
En segunda convocatoria, la realización del punto 1) Evaluación continua, no tiene recuperación y mantendrán la calificación obtenida.
El examen final deberá realizarse de nuevo.


