FUNDAMENTOS MATEMÁTICOS DE LA INGENIERÍA III
GRADO EN INGENIERÍA CIVIL
Curso 2019/2020
1. Datos de la asignatura
(Fecha última modificación: 19-03-19 21:04)- Código
- 106209
- Plan
- ECTS
- 6.00
- Carácter
- BÁSICA
- Curso
- 2
- Periodicidad
- Primer Semestre
- Idioma
- ESPAÑOL
- Área
- MATEMÁTICA APLICADA
- Departamento
- Matemática Aplicada
- Plataforma Virtual
Datos del profesorado
- Profesor/Profesora
- Manuel Domínguez Valverde
- Grupo/s
- 1
- Centro
- E. Politécnica Superior de Zamora
- Departamento
- Matemática Aplicada
- Área
- Matemática Aplicada
- Despacho
- 211 (Edificio Politécnica)
- Horario de tutorías
- Consultar: http://poliz.usal.es/politecnica/v1r00/?m=Tutorias
- URL Web
- -
- mdv@usal.es
- Teléfono
- 980 545000 Ext.3740
2. Sentido de la materia en el plan de estudios
Bloque formativo al que pertenece la materia.
Forma parte de la materia Matemáticas, junto con las asignaturas de Fundamentos Matemáticos I y II.
Papel de la asignatura.
Aportar los fundamentos matemáticos básicos del Cálculo Infinitesimal de varias variables, del Cálculo Numérico y de las Ecuaciones Diferenciales, que complementan y amplían los conocimientos que poseían de las enseñanzas previas.
Hacer constar, mediante ejemplos prácticos, la presencia de estos contenidos en la Ingeniería y por lo tanto, la repercusión de un buen manejo y comprensión de los mismos para su prelación para su futura labor profesional.
Introducir al alumno en algunas de las herramientas más utilizadas para resolver numéricamente muchos de los problemas planteados durante el curso y que también surgirán en otras asignaturas
Perfil profesional.
El seguimiento correcto de esta asignatura permitirá alcanzar al alumnado una formación matemática básica de indudable interés para su ejercicio profesional desde el punto de vista instrumental.
3. Recomendaciones previas
Son necesarios los conocimientos de matemáticas adquiridos en las asignaturas de Fundamentos Matemáticos I y II
4. Objetivo de la asignatura
OBJETIVOS GENERALES:
- Modelizar situaciones sencillas y aplicar las técnicas adecuadas para la solución del problema planteado.
- Utilizar técnicas matemáticas exactas y aproximadas.
- Interpretar las soluciones en términos matemáticos en el contexto del problema real planteado
OBJETIVOS ESPECÍFICOS
- Conseguir un dominio en las técnicas de integración múltiple
- Conocer los métodos de resolución de ecuaciones diferenciales ordinarias
- Conocer los métodos numéricos para la resolución de ecuaciones, diferenciación e integración, así como para la resolución numérica de ecuaciones diferenciales
5. Contenidos
Teoría.
Tema 1: Cálculo integral en  : Revisión/Ampliación.
: Revisión/Ampliación.
Tema 2: Introducción a las Ecuaciones Diferenciales. Modelización.
Tema 3: Ecuaciones Diferenciales Ordinarias.
Tema 4: Introducción a las Ecuaciones Diferenciales en derivadas parciales.
Tema 5: Otros métodos de resolución de Ecuaciones Diferenciales: Ejemplos y aplicaciones en Ingeniería
Tema 6: Métodos Numéricos
- 6.1.- Métodos Numéricos del Cálculo en una y varias variables
6.2.- Resolución Numérica de Ecuaciones Diferenciales
6. Competencias a adquirir
Básicas / Generales.
CB 1. Que los alumnos hayan demostrado poseer y comprender conocimientos en un área de estudio que parte de la base de la educación secundaria general y se suele encontrar a un nivel que, si bien se apoya en libros de texto avanzados, incluye también algunos aspectos que implican conocimientos procedentes de la vanguardia de su campo de estudio
CB 2. Que los estudiantes sepan aplicar sus conocimientos a su trabajo o vocación de una forma profesional y posean las competencias que suelen demostrarse por medio de la elaboración y defensa de argumentos y la resolución de problemas dentro de su área de estudio.
CB 4. Que los estudiantes puedan transmitir información, ideas, problemas y soluciones a un público, tanto especializado como no especializado.
Específicas.
CE.1 Aptitud para aplicar los conocimientos sobre: cálculo integral en varias variables, ecuaciones diferenciales, métodos numéricos, algorítmica numérica.
7. Metodologías
La metodología a seguir cubre diferentes apartados. Por un lado se expondrán brevemente los fundamentos teóricos necesarios para entender las técnicas matemáticas que se han de emplear posteriormente en la resolución de problemas.
La resolución de problemas reales exigirá la utilización de software matemático específico (Mathematica).
Todo el material didáctico necesario se pondrá a disposición de los alumnos a través de studium
Los libros básicos que los alumnos han de utilizar están a su disposición en la Biblioteca del Campus.
Para fomentar el trabajo en equipo, la realización de los trabajos se llevará a cabo en grupos de hasta 3 alumnos.
8. Previsión de Técnicas (Estrategias) Docentes
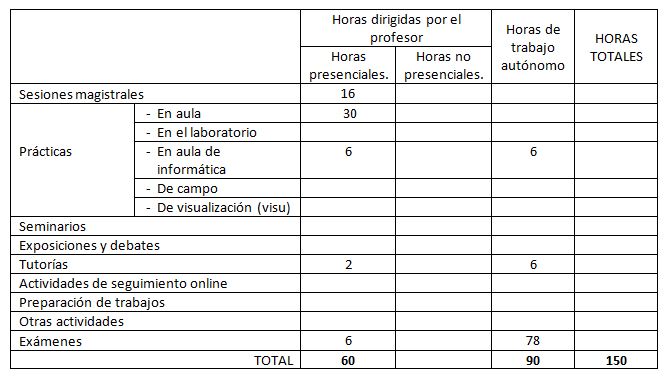
9. Recursos
Libros de consulta para el alumno.
Danko y Popov, Ejercicios y problemas de Matemáticas superiores (Ed. Paraninfo)
Demidovich, Problemas y ejercicios (Ed. Paraninfol)
Frank Ayres, Ecuaciones diferenciales, (Ed M. Graw Hill)
García, A. y García, F., Cálculo I (Ed. Clagsa)
García, A, Rodríguez, G, Ecuaciones diferenciales ordinarias, (Ed. Clagsa)
Marcellan,F; Cassasús,L; Zarzo, A. Ecuaciones diferenciales, Mc Graw Hill, 1990
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
La bibliografía y enlaces de Internet útiles se comentarán en detalle a lo largo del curso con otros contenidos de interés por su carácter clásico, novedoso, su aportación en las aplicaciones, etc.
10. Evaluación
Consideraciones generales.
Los procedimientos de evaluación miden la consecución de los objetivos de la asignatura. Además de los trabajos presentados por los alumnos sobre algunos aspectos teóricos y prácticos relacionados con la asignatura, se valorará el resultado de los exámenes presenciales cuyo formato se detalla más abajo.
Criterios de evaluación.
Valorar las técnicas exactas y aproximadas adecuadas para resolver los problemas planteados.
Valorar claridad y rigor de argumentaciones empleadas.
Se valorarán participación activa en el aula y la asistencia a las actividades complementarias.
Instrumentos de evaluación.
En la evaluación de las competencias adquiridas, se evaluará el resultado de pruebas escritas de carácter teórico-práctico, así como la asistencia a las tutorías y la participación activa en las clases. El peso sobre la calificación global de cada uno de los instrumentos de evaluación será:
Examen de conocimientos generales:….........80-90 %..
Participación en clases y tutorías………….…10- 20%.
Recomendaciones para la evaluación.
Realizar durante las horas de trabajo autónomo de los alumnos las actividades sugeridas por el profesor en el aula.
Asistir a clase y utilizar las tutorías es una actividad fundamental para el correcto seguimiento de la asignatura.
Recomendaciones para la recuperación.
Asistir a una tutoría personalizada con el profesor de la asignatura para aquellos alumnos presentados que no superen la asignatura. En dicha tutoría se realizará una programación de las actividades del alumno para alcanzar las competencias de esta asignatura.


