MECANICA TEORICA
GRADO EN FISICA
Curso 2020/2021
1. Datos de la asignatura
(Fecha última modificación: 28-07-20 10:15)- Código
- 100824
- Plan
- ECTS
- 4.50
- Carácter
- OBLIGATORIA
- Curso
- 3
- Periodicidad
- Primer Semestre
- Idioma
- ESPAÑOL
- Área
- FÍSICA TEÓRICA
- Departamento
- Física Fundamental
- Plataforma Virtual
Datos del profesorado
- Coordinador/Coordinadora
- María Pilar García Estévez
- Grupo/s
- 1
- Centro
- Fac. Ciencias
- Departamento
- Física Fundamental
- Área
- Física Teórica
- Despacho
- T3346
- Horario de tutorías
- Concretar por mail con la/s profesor/as
- URL Web
- -
- pilar@usal.es
- Teléfono
- 4435
- Profesor/Profesora
- Paz Albares Vicente (Colab.Predoctoral)
- Grupo/s
- 1
- Centro
- Fac. Ciencias
- Departamento
- Pendiente de Asignación
- Área
- Sin Determinar
- Despacho
- Despacho de becarios. Primera planta
- Horario de tutorías
- Concretar por mail con la/s profesor/as
- URL Web
- http://lbt.usal.es/staff-member/paz-albares-vicente/
- paz.albares@usal.es
- Teléfono
- 923 294435
2. Sentido de la materia en el plan de estudios
Bloque formativo al que pertenece la materia.
Módulo de Mecánica
Papel de la asignatura.
La asignatura, como parte integrante del bloque formativo de Física, pretende que los alumnos obtengan un conocimiento y competencias básicas en el ámbito de la Mecánica Teórica.
Perfil profesional.
- Docencia Universitaria o Investigación
- Docencia no universitaria
- Administración pública
- Empresas de Banca, Finanzas y Seguros
- Consultorías
- Empresas de Informática y telecomunicaciones
- Industria
3. Recomendaciones previas
Haber cursado previamente Mecánica I y II y Ecuaciones diferenciales de segundo curso.
4. Objetivo de la asignatura
- Conocer el concepto de transformación canónica y saber utilizarlo para resolver
- problemas.
- Familiarizarse con el formalismo de Hamilton-Jacobi, así como el de variables de
- acción-ángulo para resolver problemas dinámicos, y ser capaz de utilizarlos en teoría de perturbaciones
- Conocer el concepto de sistema dinámico y de caos.
- Estar familiarizado con la mecánica de medios continuos, así como conocer y saber
- Aplicar el formalismo Lagrangiano para campos.
- Comprender la importancia de las simetrías de un sistema lagrangiano asi como del teorema de Noether
-Generales:
- Comprender los principales conceptos de la Física y su articulación en leyes, teoría y modelos, valorando el papel que desempeñan en el desarrollo de la sociedad.
- Ser capaz de resolver problemas físicos obteniendo una descripción no solo cualitativa sino cuantitativa y con el grado de precisión que sea requerido del fenómenos físico en cuestión
- Desarrollar en los alumnos las habilidades de pensamiento prácticas y manipulativas propias de método científico de modo que les capaciten para llevar a cabo un trabajo investigador.
- Aprender de manera autónoma nuevos conocimientos y técnicas.
- Valorar las aportaciones de la Física a la tecnología y la sociedad.
-Específicos:
- Aplicación de los conocimientos a la práctica
- Visualización e interpretación de soluciones
- Expresión rigurosa y clara
- Razonamiento lógico e identificación de errores en los procedimientos
-Instrumentales:
- Razonamiento crítico
- Capacidad de aplicar conocimientos a la práctica
- Habilidad para trabajar autónomamente
- Destreza para usar las TICs (Tecnologías de la Información y Comunicación) para encontrar información
5. Contenidos
Teoría.
Tema I. Mecánica de Lagrange y Hamilton
1. Cálculo de variaciones
2. Formulación lagrangiana
3. Sistemas potenciales:
3..1 Términos de la energ_á cinética
3..2 Potencial: Fuerzas generalizadas
4. Sistemas con ligaduras:
4..1 Ligaduras holónomas
4..2 Ligaduras no holónomas
5. Formulación Hamiltoniana
6. Transformaciones canónicas
7. Invariantes integrales de Poincaré
8. Transformacion de escala entre oscilador armonico y particula libre
Tema II. Dinámica en el espacio de fases
1. Las ecuaciones de Hamilton
2. Espacio de fases para sistemas conservativos
3. Espacio de fases para sistemas no conservativos
4. Análisis de estabilidad para sistemas con un grado de libertad
5. Ciclos límite
6. Blow up
7. atractores
7..1 El atractor de Lorenz
Tema III. Ecuación de Hamilton-Jacobi
1. Transformaciones canónicas
2. Ecuación de Hamilton-Jacobi
3. Separación de variables en la ecuación de H-J
4. Partícula en un potencial central
Tema IV. Variables acción ángulo
1. Variables de acción
2. Un grado de libertad
3. Varios grados de libertad. Separabilidad
V. Teoría de perturbaciones canónica
1. Sistemas Hamiltonianos totalmente integrables
2. Serie de perturbaciones para un grado de libertad
3. Serie de perturbaciones para varios grados de libertad
VI. Aplicaciones simplécticas. Caos en sistemas hamiltonianos
1. Toros en dos dimensiones
2. Aplicaciones simplécticas
3. Teorema de Poincaré-Birkhoff
4. Fractales
VII. Teorema de Noether
1. Simetrías del Lagrangiano
2. Teorema de Noether
VIII. Formulación canónica del electromagnetismo. Mecánica Galileana
1. Fundamentos
2. Potenciales electromagnéticos
3. Formulación canónica
4. Tensor electromagnético
5. Monopolo magnético: Una configuración peculiar
IX. Formulación canónica de electromagnetismo en Relatividad especial
1. Partícula Libre en el marco de la Relatividad
2. Comportamiento de las Ecuaciones de Maxwell en el marco de la Relatividad Especial
3. Formalismo Hamiltoniano en Relatividad Especial
4. El problema de Coulomb en Relatividad Especial
6. Competencias a adquirir
Transversales.
Transversales:
- Capacidad de manejo de nuevas tecnologías
- Capacidad lingüística
-Sistémicas:
- Aprendizaje autónomo
- Motivación por la calidad
- Capacidad de iniciativa
7. Metodologías
La metodología a seguir consistirá en una parte de clases magistrales expositivas donde se explicarán los conceptos básicos necesarios para conseguir los objetivos, de acuerdo al programa adjunto, junto con una serie de clases prácticas de resolución de problemas de modo presencial.
Además en la parte no presencial de la asignatura se podrán proponer al alumno la resolución de problemas supervisados por el profesor periódicamente que permitirán al alumno reforzar contenidos y orientarle en la consecución de las competencias previstas.
En lo que refiere a los medios formativos se llevarán a cabo por medio de clases de pizarra tradicionales con apoyo de bibliografía especializada de consulta que se propondrá al alumno junto con las plataformas Moodle para acceso a material docente digital y recursos online que el profesor estime en cada tema.
Al principio de cada tema, se subirá a studium una hoja de problemas. El objetivo es que los alumnos traten de resolverlos por su cuenta y planteen las dificultades prácticas en las clases de seminarios.
8. Previsión de Técnicas (Estrategias) Docentes
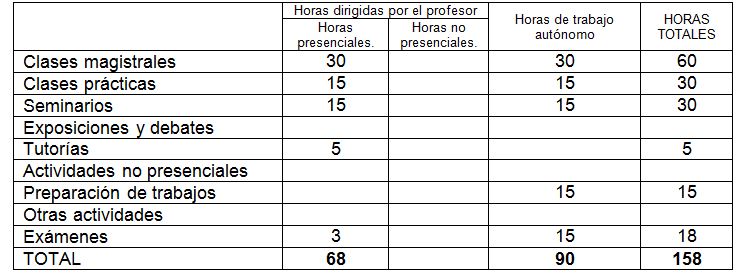
9. Recursos
Libros de consulta para el alumno.
-Classical Mechanics, Herbert Goldstein, Charles P. Poole, John L. Safko - Addison Wesley (2002) - ISBN 0201657023
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
-Classical Dynamics, J. Saletan, Cambridge University Press, 1998, ISBN 0521 636361
-Analytical mechanics, Louis N. Hand, Janet D. Finch, Cambridge University Press, 1998, ISBN 0521 57572 9
-Modern analytic mechanics, Richard Kent Cooper, C. Pellegrini, Kluwer academic, 1999, ISBN 0306459582
10. Evaluación
Consideraciones generales.
Se trata de una asignatura con un fuerte contenido teórico que permite resolver gran cantidad de problemas fisico-matematicos del mayor interés.
Criterios de evaluación.
Se valorará preferiblemente la capacidad de adaptar las enseñanzas teóricas recibidas a la resolución de problemas concretos.
Instrumentos de evaluación.
La evaluación se llevará a cabo por medio de los siguientes instrumentos, donde se explicita el porcentaje de peso de cada uno sobre la calificación final:
-Examen final presencial (70 %). Se requerirá una calificación mínima en este apartado para superar la asignatura de un 40% de la nota máxima de la prueba.
-Evaluación continua (30%) por medio de:
Dos pruebas de evaluacion-control de 15% cada una
Recomendaciones para la evaluación.
Durante el curso se recomienda a los alumnos asistir a las clases presenciales de teoría y prácticas, así como la entrega para su calificación de los ejercicios propuestos (presencial u on-line) en las fechas previstas.
Además las tutorías y seminarios colectivos serán de gran utilidad para resolver aquellas cuestiones o aclarar conceptos.
Recomendaciones para la recuperación.
Para la recuperación se recomienda contactar con el profesor para que éste le oriente en vista a reforzar o desarrollar aquellas capacidades que no hayan sido logradas.
Para aquellos alumnos que no hayan aprobado la asignatura podrán recuperar la parte del examen final presencial. El resto de las notas de evaluación continua no serán recuperables.
No obstante, si el profesor lo estima conveniente, se podrá requerir la entrega de ejercicios o trabajos propuestos para ayudar al alumno a conseguir aquellos objetivos que no hayan sido alcanzados durante el curso de la asignatura.


