MATEMÁTICAS Y SU DIDÁCTICA III
Doble Titulación Grado en Maestro Ed. Primaria e Infantil (Zamora)
Curso 2022/2023
1. Datos de la asignatura
(Fecha última modificación: 07-05-22 19:32)- Código
- 105226
- Plan
- 2016
- ECTS
- 6
- Carácter
- Curso
- 4
- Periodicidad
- Primer Semestre
- Idioma
- ESPAÑOL
- Área
- DIDÁCTICA DE LA MATEMÁTICA
- Departamento
- Did. de las Matemáticas y de las CC.EE.
- Plataforma Virtual
Datos del profesorado
- Profesor/Profesora
- María José Cáceres García
- Grupo/s
- 3
- Centro
- Fac. Ciencias de la Educación
- Departamento
- Did. de las Matemáticas y de las CC.EE.
- Área
- Didáctica de la Matemática
- Despacho
- 210
- Horario de tutorías
- 1º cuatrimestre (presencial y online): X y J de 11 a 14 horas
2º cuatrimestre (presencial y online): X y J de 9 11 y de 13 a 14 horas
- URL Web
- -
- majocac@usal.es
- Teléfono
- 980 54 50 00 Ext 3735 / 677569419
- Profesor/Profesora
- Beatriz Sánchez Barbero
- Grupo/s
- 3
- Centro
- Fac. Ciencias de la Educación
- Departamento
- Did. de las Matemáticas y de las CC.EE.
- Área
- Didáctica de la Matemática
- Despacho
- 218
- Horario de tutorías
- 1º cuatrimestre: X de 9 a 11 horas (online), J de 9 a13 horas (presencial y online)
2º cuatrimestre: X de 9 a 11 horas (online), J de 11 a 14 horas (presencial y online), V de 13 a 14 horas (presencial y online)
- URL Web
- -
- beatrizsanchezb@usal.es
- Teléfono
- 980 54 50 00 Ext. 3732 / 677 56 94 13
2. Sentido de la materia en el plan de estudios
Bloque formativo al que pertenece la materia.
Módulo Didáctico-disciplinar de Educación Primaria
Papel de la asignatura.
Permite adquirir conocimientos y capacidades tanto de Matemáticas como de su didáctica. Asume y adapta las competencias propias y las competencias Didáctico-Disciplinares de Educación Primaria (Módulo de la orden ECI/3857/2007)
Perfil profesional.
Maestro Educación Primaria
3. Recomendaciones previas
Haber cursado las asignaturas Matemáticas y su Didáctica I y Matemáticas y su Didáctica II, respectivamente, de 2º y 3º curso del Grado en Maestro en Educación Primaria.
4. Objetivo de la asignatura
- Consolidar la formación matemática necesaria acerca de los contenidos matemáticos básicos que configuran el currículo de la Educación Primaria.
- Formular problemas estadísticos
- Organizar la recogida de datos estadísticos.
- Distinguir los diferentes tipos de gráficos y tablas para realizar el posterior análisis de los datos estadísticos.
- Profundizar en el conocimiento de las diferentes medidas estadísticas.
- Abordar la Estadística a través de la Enseñanza por proyectos.
- Ampliar el conocimiento de los diferentes recursos y materiales que se pueden usar en la clase de Estadística.
- Reconocer las dificultades en el aprendizaje de la Estadística.
- Profundizar en las diferentes estrategias para abordar la enseñanza de la Estadística.
- Fomentar la capacidad de expresarse con claridad, precisión y rigor; lograr el desarrollo de competencias de autoformación y de trabajo cooperativo.
- Realizar propuestas didácticas a partir del currículo base de matemáticas en educación primaria.
- Adquirir destrezas en el empleo de los medios, materiales, y recursos usuales en la enseñanza-aprendizaje de las Matemáticas.
- Crear informes estadísticos a partir de un problema inicial.
5. Contenidos
Teoría.
Tema 1: La Enseñanza de la Estadística. Aspectos generales
Tema 2: Variables estadísticas. Tablas y gráficos
Tema 3: Medidas de tendencia central y de dispersión.
Tema 4: Dificultades en el aprendizaje de la Estadística
Tema 5: Recursos y materiales para la enseñanza de la Estadística.
Tema 6: La probabilidad y su enseñanza.
6. Competencias a adquirir
Básicas / Generales.
COMPETENCIAS BÁSICAS:
CB1. Que los estudiantes hayan demostrado poseer y comprender conocimientos en el área/s de estudio que parte de la base de la educación secundaria general, y se sueleencontrar a un nivel, que si bien se apoya en libros de texto avanzados, incluye también algunos aspectos que implican conocimientos procedentes de la vanguardia de su campo de estudio.
CB2. Que los estudiantes sepan aplicar sus conocimientos a su trabajo o vocación de una forma profesional y posean las competencias que suelen demostrarse por medio de la elaboración y defensa de argumentos y resolución de problemas dentro de su área de estudio.
CB3. Que los estudiantes tengan la capacidad de reunir e interpretar datos relevantes (normalmente dentro de su área de estudio de para emitir juicios que incluyan una reflexión sobre temas relevantes de índole social, científica o ética.
CB4. Que los estudiantes puedan transmitir información, ideas, problemas y soluciones a un público tanto especializado como no especializado.
CB5. Que los estudiantes hayan desarrollado aquellas habilidades de aprendizaje necesarias para emprender estudios posteriores con un alto grado de autonomía.
COMPETENCIAS GENERALES:
CG3.- Que los estudiantes tengan la capacidad de competencia digital, que conlleva un uso seguro y crítico de las tecnologías de la sociedad de la información (TSI) y, por tanto, el dominio de las tecnologías de la información y la comunicación (TIC).
CG4.- Que los estudiantes tengan la capacidad de aprender a aprender, competencia vinculada al aprendizaje, a la capacidad de emprender y organizar un aprendizaje ya sea individualmente o en grupos, según las necesidades propias del individuo, así como a ser conscientes de los métodos y determinar las oportunidades disponibles.
Específicas.
CE 38 DP 14 Adquirir competencias matemáticas básicas (numéricas, cálculo, geométricas, representaciones espaciales, estimación y medida, organización e interpretación de la información, etc.).
CE 39 DP 15 Conocer el currículo escolar de matemáticas.
CE 40 DP 16 Analizar, razonar y comunicar propuestas matemáticas.
CE 41 DP 17 Plantear y resolver problemas vinculados con la vida cotidiana.
CE 42 DP 18 Valorar la relación entre matemáticas y ciencias como uno de los pilares de pensamiento científico.
CE 43 DP 19 Desarrollar y evaluar contenidos del currículo mediante recursos didácticos apropiados y promover las competencias correspondientes en los estudiantes.
7. Metodologías
El desarrollo de la asignatura se estructura en torno a las siguientes actividades;
1.- Actividades formativas presenciales:
- Clases teóricas en las que se desarrollarán los contenidos del programa.
- Clases prácticas que permitan profundizar en los aspectos teóricos previos, establecer conexiones entre teoría y práctica y reflexionar acerca de la enseñanza-aprendizaje de los conceptos matemáticos.
- Seminarios/tutorías de grupo (6 alumnos máximo) en los que se orientarán y encauzarán los trabajos en equipo y se resolverán las dificultades.
- Tutorías individualizadas para profundizar en el conocimiento y para el asesoramiento, resolución de problemas y evaluación de cada alumno.
- Examen final sobre los contenidos de la asignatura.
2.- Actividades formativas no presenciales:
- Proyectos de enseñanza de la Estadística en equipo que los alumnos expondrán oralmente al resto de la clase. Se pretende mejorar la capacidad de trabajo en equipo, la creatividad, los mecanismos de búsqueda y selección de información, la comunicación oral, la toma de decisiones, el aprendizaje autónomo, la capacidad de planificación y el manejo de tecnologías de la información y comunicación. Los alumnos podrán escoger el trabajo entre un listado propuesto al inicio del curso.
- Realización de actividades para cada tema en la plataforma Studium de la Universidad de Salamanca
- Preparación de pruebas de evaluación.
8. Previsión de Técnicas (Estrategias) Docentes
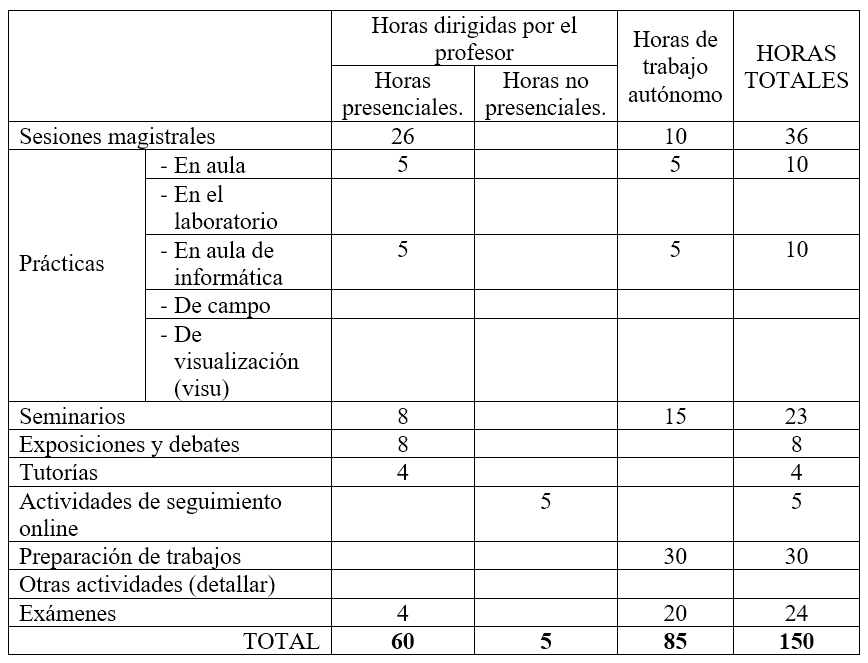
9. Recursos
Libros de consulta para el alumno.
Castro E. (ed.) (2001) Didáctica de la Matemática en Educación Primaria. Síntesis, Madrid.
Chamorro M. C. (cood) (2003) Didáctica de las Matemáticas. Pearson Prentice Hall. Madrid
Díaz Godino J. et al. (2004) Matemáticas para Maestros. Proyecto EDUMAT-Maestros.
Díaz Godino J. et al (2004) Didáctica de las Matemáticas para Maestros. Proyecto EDUMAT-Maestros. Disponibles en: http://www.ugr.es/~jgodino/edumat-maestros/welcome.htm
Flores Martínes, P. y Rico Romero, L. (coords) (2015) Enseñanza y aprendizaje de las matemáticas en Educación Primaria. Pirámide. Madrid.
Segovia Alex, I. y Rico Romero, L. (coords.) (2011) Matemáticas para maestros de educación Primaria. Pirámide. Madrid.
VVAA (2106) Didáctica de las matemáticas para maestros de educación primaria. Madrid: Editorial Paraninfo.
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
Bibliografía complementaria:
AA.VV. (1995) Monográfico “Probabilidad y Estadística”, UNO, 5.
American Statistical Association. (2002). What is a statistical project? Online: www.amstat.org/education/statproject.html.
Arteaga, P., Batanero, C., Díaz, C. y Contreras, J. M. (2009). El lenguaje de los gráficos estadísticos. UNION, 18, 93-104.
Azcárate, P. y Cardeñoso, J.M. (1996) El lenguaje del azar. Una visión fenomenológica sobre los juicios probabilísticos. Epsilon, 35, 12(2), pp. 165-178.
Azcárate, P. y Cardeñoso, J. M. (2001). Probabilidad. En, E. Castro (Ed.). Didáctica de la matemática en la Educación Primaria (pp. 591-619)). Madrid: Síntesis.
Castro E., Rico L., Castro E. (1988) Números y operaciones. Fundamento para una aritmética escolar. Madrid: Síntesis.
Batanero, C. (1998). Recursos en Internet para la educación estadística. UNO, 15, 13-25.
Batanero, C. (2000). Significado y comprensión de las medidas de tendencia central. UNO, 25, 41-58.
Batanero, C. y Serrano, L. (1995) La aleatoriedad, sus significados e implicaciones educativas. UNO, 5, pp. 15-28.
Borras, E. (1995) Procedimientos y recursos para trabajar al Estadística y la Probabilidad en la enseñanza. UNO, 3, 61-76.
Cañizares, M. J., Batanero, C., Serrano, L. y Ortiz, J. J. (1999). Comprensión de la idea de juego equitativo en los niños. Números, 37, 37-55.
Cañizares, M. J. y Batanero, C. (1997). Influencia del razonamiento proporcional y de las creencias subjetivas en la comparación de probabilidades. UNO, 14, 99-114.
Cardeñoso, J.M. y Azcárate, P. (1995) Tratamiento del conocimiento probabilístico en los proyectos y materiales curriculares. SUMA, 20 41-51.
Chamoso, J.; Cáceres, M. J.; Azcárate, P. y Cardeñoso, J. M. (2007): Organizando la estadística. Colección Diálogos de Matemáticas. Madrid: Nivola.
Cobo, B. y Batanero, C. (2000). La mediana en la educación secundaria obligatoria: ¿Un concepto sencillo? UNO 23, 85-96.
Díaz, J. Batanero, M.C. y Cañizares, M.J. (1987) Azar y probabilidad. Síntesis. Madrid.
Engel, A. (1988) Probabilidad y Estadística, Volumen I. Valencia: Mestral.
Hacking, I. (1991) La domesticación del azar.Gedisa. Barcelona.
Hacking, L. (1995) El surgimiento de la probabilidad. Gedisa. Barcelona.
Hernández, V. y Vélez, R. (1992) Dados, monedas y urnas. Introducción al cálculo de probabilidades. Madrid: Universidad Nacional de Educación a Distancia.
Nortes, A. (1987) Encuestas y precios. Madrid: Síntesis.
Pérez, P. (1995). Actividades de probabilidad para la enseñanza primaria. UNO, 5, 113-122.
Ross, S. (2008) Introducción a la Estadística. Barcelona: Reverté.
Sáenz, C. (1999). Materiales para la enseñanza de la teoría de probabilidades. Madrid: ICE de la Universidad Autónoma.
Serrano, L. (2009) Tendencias actuales de la investigación en Educación Estocástica. Granada: Universidad de Granada.
- Otros libros:
Libros de texto de primaria
- Recursos virtuales:
http://nlvm.usu.edu/es/ (español)
http://illuminations.nctm.org/ (inglés)
http://recursostic.educacion.es/descartes/web/ (español)
http://clic.xtec.cat/db/listact_es.jsp (español)
10. Evaluación
Consideraciones generales.
Se evaluará el grado de adquisición de las competencias de la materia. Dicha evaluación será continua y global, tendrá carácter orientador y formativo, y deberá analizar los procesos de aprendizaje individual y colectivo. La calificación deberá ser reflejo del aprendizaje individual, y contemplará la adquisición de conocimientos, la participación del alumno, tanto en actividades individuales y grupales, y los cambios intelectuales y actitudinales de los estudiantes. La adquisición de los contenidos teóricos supondrá el 60% de la calificación de la asignatura, las actividades prácticas presenciales y no presenciales el 25% y la participación activa en las actividades programadas un 15%.
Criterios de evaluación.
Se calificarán tres aspectos fundamentales de aprendizaje:
- Asistencia a clase con aprovechamiento.
- Proyectos por equipos
- El estudio por medio de los exámenes.
Instrumentos de evaluación.
La evaluación de la asignatura se realizará mediante:
- Examen final escrito.
- Los proyectos realizados en grupo que se ajustará a un esquema entregado a los alumnos al inicio de curso.
Recomendaciones para la evaluación.
La asistencia habitual dará derecho a una evaluación continua del alumno donde se valoran las distintas actividades realizadas. En otro caso la evaluación se llevará a cabo por medio de un examen final teórico de toda la materia.
El aprobado en el examen teórico-práctico y la entrega y adecuación de los trabajos individuales y en grupo serán un requisito imprescindible para aprobar la asignatura
Recomendaciones para la recuperación.
Se seguirán los mismos criterios de evaluación que en la primera convocatoria. La tutoría individual y personalizada permitirá orientar las estrategias para superar con éxito la asignatura.


