MATEMÁTICA APLICADA Y ESTADÍSTICA
GRADO EN FARMACIA
Curso 2023/2024
1. Datos de la asignatura
(Fecha última modificación: 25-05-23 17:31)- Código
- 100101
- Plan
- 201
- ECTS
- 8.00
- Carácter
- BÁSICA
- Curso
- 1
- Periodicidad
- Primer cuatrimestre
- Idioma
- ESPAÑOL
- Área
- ESTADÍSTICA E INVESTIGACIÓN OPERATIVA
- Departamento
- Estadística
- Plataforma Virtual
Datos del profesorado
- Coordinador/Coordinadora
- Rosa Amanda Sepúlveda Correa
- Grupo/s
- 1, 2, 3 y 4
- Centro
- Fac. Medicina
- Departamento
- Estadística
- Área
- Estadística e Investigación Operativa
- Despacho
- 3.15 Facultad de Medicina
- Horario de tutorías
- Lunes, martes y jueves de 12:00 a 14:00
- URL Web
- https://produccioncientifica.usal.es/investigadores/57431/detalle
- rsepulveda@usal.es
- Teléfono
- 663089749 Ext. 6989
- Profesor/Profesora
- Nerea González García
- Grupo/s
- 1, 2, 3 y 4
- Centro
- Fac. Economía y Empresa
- Departamento
- Estadística
- Área
- Estadística e Investigación Operativa
- Despacho
- Facultad de Medicina (segunda planta). Despacho 3.6.2
- Horario de tutorías
- Lunes y Viernes de 9:00 a 12:00 (cita previa)
- URL Web
- https://produccioncientifica.usal.es/investigadores/57945/detalle
- nerea_gonzalez_garcia@usal.es
- Teléfono
- 923 294500 Ext. 6999
- Profesor/Profesora
- Antonio Blázquez Zaballos
- Grupo/s
- 1, 2, 3 y 4
- Centro
- Fac. Economía y Empresa
- Departamento
- Estadística
- Área
- Estadística e Investigación Operativa
- Despacho
- Facultad de Medicina (segunda planta). Despacho 3.13
- Horario de tutorías
- Miércoles de 9.00 a 12.00 (preferible con cita previa)
- URL Web
- https://produccioncientifica.usal.es/investigadores/56166/detalle
- abz@usal.es
- Teléfono
- 923 294500 ext. 6986
- Profesor/Profesora
- María José Fernández Gómez
- Grupo/s
- 1, 2, 3 y 4
- Centro
- Fac. Biología
- Departamento
- Estadística
- Área
- Estadística e Investigación Operativa
- Despacho
- 3.3 Facultad de Medicina
- Horario de tutorías
- Escribir un correo para cita previa
- URL Web
- https://produccioncientifica.usal.es/investigadores/56898/detalle
- mjfg@usal.es
- Teléfono
- EXT. 6984
2. Sentido de la materia en el plan de estudios
Bloque formativo al que pertenece la materia.
Ciencias Básicas: Física y Matemáticas.
Papel de la asignatura.
En su formación específica el futuro farmacéutico requerirá las matemáticas y la estadística como herramienta, desde el primer cuatrimestre del curso en otras asignaturas tales como Física Aplicada, Físico Química, Biofarmacia y Farmacocinética, Química Inorgánica, Técnicas Instrumentales, entre otras.
Además, una de las competencias del futuro farmacéutico es el análisis de datos y la manipulación de diversas sustancias teniendo en cuenta sus propiedades físicas y químicas, dentro de lo cual la estadística y/o las matemáticas juegan un papel fundamental.
Perfil profesional.
La salida profesional más frecuente para los licenciados en esta carrera es la Oficina de Farmacia, cuya labor exige una base científica y técnica importante. Por otro lado, los laboratorios demandan un gran número de licenciados para ocupar puestos de responsabilidad en producción y control de calidad. Si bien la investigación es una salida de difícil acceso para cualquier licenciado, el número de licenciados en farmacia dedicados a la investigación es muy alto en comparación con otros campos, por ello las universidades deben aportar una sólida formación científica y técnica.
En términos generales, dentro de las competencias del farmacéutico, se recoge la capacidad de realizar ensayos de productos medicinales, su diseño, su observación, clasificación, contraste, análisis de la información, toma de decisiones, etc. Competencias que desarrolla esta asignatura para la gran cantidad de situaciones en las que intervienen funciones o ecuaciones que relacionen algunas de las magnitudes en estudio o distintos conceptos estadísticos que consideran relaciones aleatorias entre las magnitudes.es.
3. Recomendaciones previas
Es recomendable que el alumno haya cursado la asignatura de Matemáticas en los dos años de Bachillerato.
4. Objetivo de la asignatura
Generales
Proporcionar a los alumnos de primer año de Farmacia conocimientos básicos en Cálculo Diferencial, Ecuaciones Diferenciales, Estadística Descriptiva y Estadística Inferencial, que les sean de utilidad en materias posteriores y en su desarrollo profesional. De esta forma, el futuro farmacéutico tendrá una visión científico- matemática determinista y aleatoria de fenómenos propios del área, así como de la resolución de problemas relacionados con estos fenómenos.
Específicos
- Adquirir destreza tanto en el cálculo como en la aplicación de los conceptos de derivadas, diferenciales y derivadas parciales.
- Reconocer y resolver los tipos más básicos de ecuaciones diferenciales, así como su aplicación en distintos campos de la ciencia, especialmente de aquellos afines a las ciencias farmacéuticas.
- Adquirir la capacidad de ordenación y descripción gráfica de un conjunto de datos.
- Resumir un conjunto de datos utilizando un conjunto de medidas numéricas (estadísticos).
- Utilización y correcta aplicación del modelo de regresión lineal bajo un punto de vista descriptivo.
- Comprender el concepto de intervalo de confianza.
- Diferenciar el concepto de probabilidad y confianza en el contexto de intervalos.
- Aplicar los intervalos de confianza en función de las características de las muestras y el parámetro a estimar.
- Calcular el tamaño muestral necesario para obtener un intervalo de confianza dado un error determinado.
- Definir los conceptos básicos para la formulación de un contraste de hipótesis
- Comprender los posibles errores que se pueden producir en un contraste de hipótesis
- Definir nivel de significación en contrastes de hipótesis
- Comprender el significado de un p-valor en un contraste de hipótesis.
- Aplicar los contrastes de hipótesis en función del objetivo de un experimento y la información que se tiene de la población o poblaciones en estudio.
- Comprender el concepto de potencia de un contraste de hipótesis.
- Diferenciar entre contrastes paramétricos y no paramétricos.
- Utilizar los contrastes de independencia y homogeneidad para el análisis de las relaciones existentes entre dos variables cualitativas.
- Discutir la utilización de contrastes por parejas cuando se trabaja con más de dos poblaciones.
- Introducir al alumno en los diseños experimentales para comparar más de dos tratamientos.
5. Contenidos
Teoría.
PARTE 1: CÁLCULO DIFERENCIAL E INTEGRAL.
Tema 1: Concepto de diferencial. Aplicaciones.
Tema 2: La integral definida. Cálculo de primitivas. Aplicaciones.
Tema 3: Introducción a las funciones de varias variables. Derivadas parciales y diferenciales.
PARTE 2: ECUACIONES DIFERENCIALES.
Tema 4: Introducción a las ecuaciones diferenciales. Resolución de ecuaciones diferenciales de primer orden. Aplicaciones.
Tema 5: Ecuaciones diferenciales como modelos matemáticos: planteamiento de ecuaciones diferenciales de primer orden.
PARTE 3: ESTADÍSTICA DESCRIPTIVA.
Tema 6: Variables y escalas de medida. Tablas de frecuencias. Representaciones gráficas.
Tema 7: Descripción de una muestra: Medidas de tendencia central, posición, dispersión y forma. Gráficos asociados.
Tema 8: Análisis de Regresión y Correlación: Distribuciones estadísticas bidimensionales. Covarianza. Coeficiente de correlación lineal de Pearson. Regresión lineal mínimo cuadrática. Estudio de la representatividad de la recta de regresión.
PARTE 4: ESTADÍSTICA INFERENCIAL.
Tema 9: Nociones básicas de probabilidad. Aplicaciones del teorema de Bayes y de la Probabilidad Total a los test de diagnósticos clínicos.
Tema 10: Distribuciones de probabilidad. Distribuciones discretas: La distribución binomial. Distribuciones continuas: la distribución normal y distribuciones asociadas (Chi-cuadrado de Pearson, T de Student y F de Snedecor).
Tema 11: Muestreo. Estimación puntual. Propiedades de los estimadores.
Tema 12: Estimación por intervalos de confianza. Determinación del tamaño muestral.
Tema 13: Contraste de Hipótesis para una y dos poblaciones.
Tema 14: Análisis de Tablas de contingencia.
Tema 15: Análisis de la Varianza (ANOVA).
6. Competencias a adquirir
Básicas / Generales.
CB1 - Que los estudiantes hayan demostrado poseer y comprender conocimientos en un área de estudio que parte de la base de la educación secundaria general, y se suele encontrar a un nivel que, si bien se apoya en libros de texto avanzados, incluye también algunos aspectos que implican conocimientos procedentes de la vanguardia de su campo de estudio.
CB2 - Que los estudiantes sepan aplicar sus conocimientos a su trabajo o vocación de una forma profesional y posean las competencias que suelen demostrarse por medio de la elaboración y defensa de argumentos y la resolución de problemas dentro de su área de estudio.
CB3 - Que los estudiantes tengan la capacidad de reunir e interpretar datos relevantes (normalmente dentro de su área de estudio) para emitir juicios que incluyan una reflexión sobre temas relevantes de índole social, científica o ética.
CB4 - Que los estudiantes puedan transmitir información, ideas, problemas y soluciones a un público tanto especializado como no especializado.
CB5 - Que los estudiantes hayan desarrollado aquellas habilidades de aprendizaje necesarias para emprender estudios posteriores con un alto grado de autonomía.
CG-1 - Reconocer las propias limitaciones y la necesidad de mantener y actualizar la competencia profesional, prestando especial importancia al autoaprendizaje de nuevos conocimientos basándose en la evidencia científica disponible
Específicas.
CE3 - Saber aplicar el método científico y adquirir habilidades en el manejo de la legislación, fuentes de información, bibliografía, elaboración de protocolos y demás aspectos que se consideran necesarios para el diseño y evaluación crítica de ensayos preclínicos y clínicos.
CEM2-1 - Aplicar los conocimientos de Física y Matemáticas a las ciencias farmacéuticas.
CEM2-2 - Aplicar técnicas computacionales y de procesamiento de datos, en relación con información referente a datos físicos, químicos y biológicos.
CEM2-3 - Diseñar experimentos en base a criterios estadísticos.
CEM2-4 - Evaluar datos científicos relacionados con los medicamentos y productos sanitarios.
CEM2-5 - Utilizar el análisis estadístico aplicado a las ciencias farmacéuticas.
7. Metodologías
- Clases expositivas de los contenidos teóricos de la asignatura. El material relativo a estas clases, estará disponible para los alumnos en la plataforma Studium.
- Sesiones de seminarios para la resolución de ejercicios y problemas. El material para estas sesiones estará disponible para los alumnos en la plataforma Studium.
- Clases de ordenador. El material para las prácticas estará disponible para los alumnos en la plataforma Studium
8. Previsión de Técnicas (Estrategias) Docentes
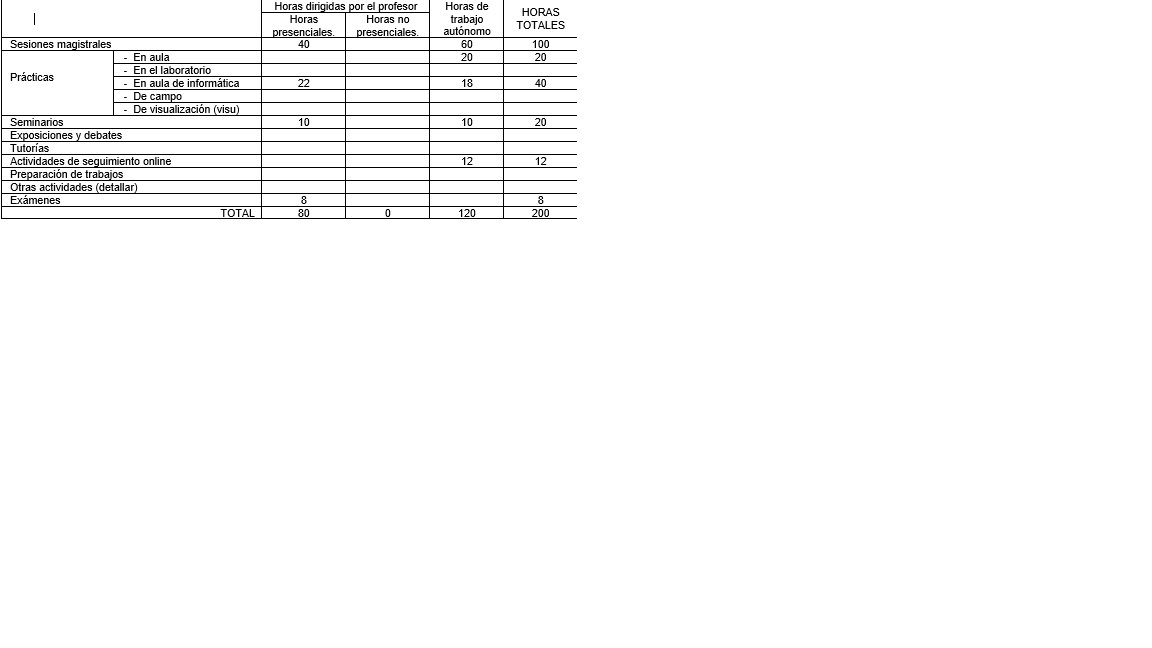
9. Recursos
Libros de consulta para el alumno.
- Ríus Díaz, F., Barón López, F. J., Sánchez Font, E., y Parras Guijosa, L. (2005). Bioestadística: métodos y aplicaciones. Universidad de Málaga. Thomsom, Madrid. (Disponible en la página web: http://www.bioestadistica.uma.es/libro/ ).
- Sánchez, M., Frutos, G. y Cuesta, P. (2007). Estadística y Matemáticas Aplicadas: Edición dirigida a los estudios de farmacia. Editorial Síntesis, Madrid.
- Zill, D. G. (2002). Ecuaciones diferenciales con aplicaciones de modelado. International Thomson, México D. F.
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
- Anton, H. (1999). Calculus: a new horizon. John Wiley & Sons, New York.
- Ayres, F. (2000). Ecuaciones diferenciales. McGraw-Hill, México D. F.
- Bradley, G. L. (2000). Cálculo vol. II: de varias variables. Prentice Hall, Madrid.
- Demidovich B. (1982). Problemas y Ejercicios de Análisis Matemático. Ed. Paraninfo, Madrid.
- Galindo, M.P. (1984). Exposición intuitiva de métodos estadísticos. Fundamentos y aplicaciones a biología, medicina y otras ciencias. Editorial Universidad de Salamanca, Salamanca.
- Martín, A. y Luna del Castillo, J. (2004). Bioestadística para las ciencias de la salud. Capitel ediciones, Madrid. .
- Thomas, G. B. (2006). Cálculo: varias variables. Pearson Educación, México D F
- Tomeo Perucha, V., y Juaréz Uña, I. (2003). Lecciones de estadística descriptiva: curso teórico-práctico. Thomson, Madrid.
- Valderrama-Bonnet, M. J. (1989). Métodos matemáticos aplicados a las ciencias experimentales. Pirámide, Madrid.
10. Evaluación
Consideraciones generales.
La asignatura tiene dos partes bien diferenciadas, Matemáticas y Estadística.
- La prueba de evaluación de Matemáticas consiste en la resolución/desarrollo de problemas.
- En la prueba de evaluación de Estadística se realizará un examen tipo test para conocer el nivel de conocimientos de los métodos contemplados en el programa de forma exhaustiva y se realizará un examen de prácticas con ordenador donde el alumno ha de poner de manifiesto que ha adquirido la destreza necesaria para seleccionar las pruebas estadísticas más adecuadas y evaluar las estadísticas biomédicas de forma crítica.
Criterios de evaluación.
MATEMÁTICAS
- Evaluación continua: participación en actividades formativas, 5%.
- Examen escrito: 30% (resolución de problemas) (CE3, CEM2-1, CEM2-4)
ESTADÍSTICA
- Actividades de prácticas de ordenador: 10% (CEM2-2, CEM2-4, CEM2-5).
- Actividades teórico/prácticas: 10% (CEM2-1, CEM2-3, CEM2-4, CEM2-5)
- Examen escrito (45%) que constará de dos partes:
- Test Teórico/Práctico: 25% (CEM2-1, CEM2-3, CEM2-4, CEM2-5).
- Prácticas en Ordenador: 20% (CEM2-2, CEM2-4, CEM2-5).
Para aprobar la asignatura se exigirá:
- Un mínimo de 3.5 puntos sobre 10 en cada uno de los exámenes (examen escrito de matemáticas y examen escrito de estadística). En caso de no cumplir este requisito, la calificación final máxima será de 4 puntos.
- Una media ponderada superior o igual a 5.0 puntos.
Se considerará la calificación de NP (No Presentado), si el estudiante no ha realizado cualquiera de las pruebas de evaluación.
Instrumentos de evaluación.
Pruebas escritas.
Actividades online.
Recomendaciones para la evaluación.
- Asistir tanto a las clases teóricas como a las prácticas.
- Resolver de forma sistemática las guías de ejercicios que se van proporcionando en los distintos temas.
- Manejar el material de apoyo y las prácticas virtuales disponibles en Studium
- Utilizar la bibliografía para afianzar conocimientos y, si es necesario, adquirir una mayor destreza en la materia.
- Acudir a las tutorías para resolver las diversas dudas que puedan surgir a lo largo del curso.
Recomendaciones para la recuperación.
La calificación en evaluación continua (25%) correspondiente a participación en actividades formativas, en actividades prácticas de ordenador y de teoría, no es recuperable.
En caso de no aprobar la asignatura en primera convocatoria, deberá presentarse en segunda convocatoria a los exámenes escritos de matemáticas y estadística.
La calificación de esta segunda convocatoria corresponde al examen escrito de matemáticas (30%), al examen escrito de estadística (teoría y prácticas con ordenador, 45%) y a la evaluación continua (25%).


