MATEMÁTICA APLICADA II
GRADO EN ARQUITECTURA TÉCNICA
Curso 2025/2026
1. Datos de la asignatura
(Fecha última modificación: 02-06-25 11:44)- Código
- 101005
- Plan
- ECTS
- 6.00
- Carácter
- BÁSICA
- Curso
- 1
- Periodicidad
- Segundo Semestre
- Idioma
- ESPAÑOL
- Área
- MATEMÁTICA APLICADA
- Departamento
- Matemática Aplicada
- Plataforma Virtual
Datos del profesorado
- Profesor/Profesora
- Manuel Vidal Vielma Blanco
- Grupo/s
- 1
- Centro
- E. Politécnica Superior de Zamora
- Departamento
- Matemática Aplicada
- Área
- Matemática Aplicada
- Despacho
- Despacho 219. Edificio Politécnica
- Horario de tutorías
- Lunes: 11:00 a 14:00
Despacho 219. Edificio Politécnica
- URL Web
- https://produccioncientifica.usal.es/investigadores/823549/detalle
- manuel.vielma@usal.es
- Teléfono
- 923 294500 Ext. 3741
2. Recomendaciones previas
Son necesarios los conocimientos y las técnicas matemáticas y científicas básicas adquiridas en la etapa previa a la Universidad. Se necesitan por tanto, conocimientos básicos tanto de Álgebra Lineal (matrices, sistemas de ecuaciones, habilidades de cálculo básico) como de estadística descriptiva. Las posibles deficiencias que el alumnado posea en su formación inicial (a nivel de Bachillerato, Formación Profesional, etc.) se resolverán mediante la asistencia a las tutorías individuales o colectivas, o mediante seminarios específicos si la situación así lo requiere.
3. Objetivos
OBJETIVOS GENERALES:
– Modelizar situaciones sencillas y aplicar las técnicas adecuadas para la solución del problema planteado.
– Utilizar técnicas matemáticas exactas y aproximadas.
– Interpretar las soluciones en términos matemáticos en el contexto del problema real planteado.
OBJETIVOS ESPECÍFICOS:
– Resolver problemas básicos de cálculo matricial y aplicarlos a la resolución de problemas.
– Plantear, analizar y resolver adecuadamente casos diversos de sistemas de ecuaciones lineales.
– Conocer los criterios y técnicas adecuados para la diagonalización de una matriz.
– Estudiar posiciones relativas de variedades afines en el espacio y resolver diversos problemas métricos.
– Estudiar diferentes lugares geométricos en el plano y en el espacio.
– Conocer y hallar los parámetros más usados en estadística descriptiva, tanto de medidas de centralización como de dispersión.
– Realizar adecuadamente el estudio de dos variables, su correlación y regresión.
– Manejar adecuadamente distribuciones discretas y continuas.
– Plantear y resolver problemas de contraste de hipótesis.
– Resolver problemas de optimización.
4. Competencias a adquirir | Resultados de Aprendizaje
Básicas / Generales | Conocimientos.
- Capacidad de razonamiento, discusión y exposición de ideas propias.
- Capacidad de búsqueda, análisis, y selección de información.
Específicas | Habilidades.
- Aptitud para utilizar los conocimientos aplicados relacionados con el cálculo numérico e infinitesimal, el álgebra lineal, la geometría analítica y diferencial, y las técnicas y métodos probabilísticos y de análisis estadístico.
Transversales | Competencias.
- Capacidad de organización y planificación
- Resolución de problemas
- Trabajo en equipo
- Aprendizaje autónomo
5. Contenidos
Teoría.
BLOQUE I: ÁLGEBRA LINEAL
Parte I : Cálculo matricial
- Matrices
- Sistemas de ecuaciones lineales
- Diagonalización
Parte II: Geometría
- Espacio afín
- Espacio euclídeo
- Cónicas
BLOQUE II: ESTADÍSTICA
Parte III: Estadística y probabilidad
- Estudio de una variable
- Estudio de dos variables
- Combinatoria y probabilidad
6. Metodologías Docentes
La metodología docente se enfoca a la resolución de problemas, aunque obviamente en las clases magistrales se exponen los fundamentos teóricos mínimos necesarios para una correcta comprensión de los diferentes algoritmos de resolución de problemas que se utilizan a lo largo del semestre.
En consecuencia, la mayoría de las actividades realizadas en el aula son de carácter práctico, con la resolución por parte del profesor y de los alumnos de numerosos problemas que permitan adquirir las competencias fijadas para esta asignatura.
Un apartado importante en esta asignatura lo constituyen las prácticas de laboratorio usando el paquete Mathematica. Estas prácticas se realizan en grupos medianos (dependiendo de la capacidad del aula asignada), aunque la formación se completa con el trabajo individual de los alumnos, aprovechando la licencia campus de Mathematica que la Universidad de Salamanca tiene.
En consecuencia, las actividades presenciales de los alumnos se orientan a la resolución de problemas y a la utilización de un software matemático avanzado que les permita abordar cálculos complicados.
Los materiales docentes están a disposición de los alumnos de la plataforma Studium de la Universidad de Salamanca.
Los alumnos han de elaborar, individualmente y en grupos muy reducidos, una serie de trabajos que permitan su evaluación. También se realizarán exámenes presenciales (uno cada mes, aproximadamente) en la hora de clase.
7. Distribución de las Metodologías Docentes
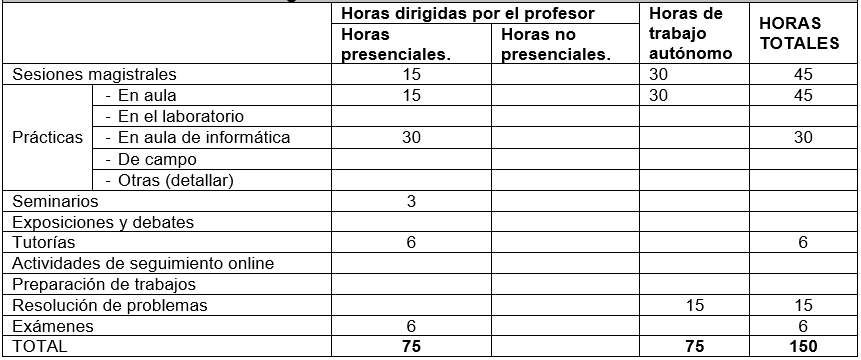
8. Recursos
Libros de consulta para el alumno.
Bibliografía Básica:
1-Álgebra y Geometría
- DE LA VILLA. Problemas de Álgebra con esquemas teóricos. Clagsa.
2-Estadística y Probabilidad:
- S.J. ÁLVAREZ CONTRERAS. Estadística Aplicada. Teoría y problemas. Clagsa
- Q. MARTÍN, M.T CABERO, Y. DE PAZ. Tratamiento estadístico de datos con SPSS. Paraninfo.
Bibliografía de ampliación:
1-Álgebra y Geometría:
- B. KOLMAN; Álgebra lineal con aplicaciones y MATLAB. Prentice Hall.
- D.C. LAY, Álgebra Lineal y sus aplicaciones. Pearson Education.
- R. BENAVENT, Cuestiones sobre Álgebra Lineal. Paraninfo
2-Estadística y Probabilidad
- J.L DEVORE. Probabilidad y estadística para ingeniería y ciencias. Thompson
S. M. ROSS, Introducción a la Estadística. Reverté.
9. Evaluación
Criterios de evaluación.
En los exámenes parciales y/o finales:
-Se valorará la adecuación de las técnicas exactas y aproximadas utilizadas para resolver los problemas planteados.
-Se valorará la claridad y rigor de las argumentaciones realizadas.
-No se tendrán en cuenta los errores de cálculo salvo que denoten desconocimiento de la materia, sean repetidos y/o impidan la correcta interpretación de los problemas que se debían resolver.
En la realización de las prácticas con Mathematica, se valorará el trabajo personal del alumno, la corrección de las técnicas empleada y la correcta resolución de los problemas planteados.
Sistemas de evaluación.
Examen parcial eliminatorio (teoría)
- Temario: temas 1 al 3
- Valor: 30%
Examen práctico (Mathematica)
- Temario: el de las prácticas 1 - 6
- Valor: 30%
Examen final (convocatoria ordinaria)
- Temario: temas 1 al 9 (teoría). Los estudiantes que hayan aprobado el examen parcial sólo deben presentarse a los temas 4 - 9.
- Valor: 70% para los nueve temas. 40% si son sólo los temas 4 - 9
Los exámenes teóricos tendrán una duración de dos horas y constarán en la resolución de problemas. Los exámenes prácticos se realizarán con el programa Mathematica en el aula de informática
En el caso de no superar la asignatura en primera convocatoria, el procedimiento de recuperación consistirá en la realización de un examen presencial con la totalidad del contenido teórico en la convocatoria extraordinaria. El contenido práctico no se recupera ni en la convocatoria ordinaria ni en la extraordinaria.
Finalmente, hay que hacer constar las razones por las que la calificación de un alumno será la de “Alumno sin calificar” o bien de “Alumno No Presentado”: La no realización de los exámenes programados.
Recomendaciones para la evaluación.
Los procedimientos de evaluación miden la consecución de los objetivos de la asignatura, y se basan en dos aspectos: por una parte, la valoración del trabajo personal de los alumnos sobre algunos aspectos teóricos y prácticos relacionados con la asignatura; y por otra parte el resultado de los exámenes parciales o finales, de tipo presencial.
RECOMENDACIONES PARA LA EVALUACIÓN.
Para obtener la calificación relacionada con el trabajo personal de los alumnos, es necesario realizar de forma continuada y en las fechas previstas las actividades propuestas por el profesor. La asistencia a las prácticas en laboratorio es necesaria para la correcta resolución de las prácticas propuestas referidas a la utilización de Mathematica.
Para obtener la calificación relacionada con los exámenes parciales, hay que realizar correctamente las cuestiones propuestas, mostrando un buen planteamiento del problema, haciendo una buena elección de las técnicas adecuadas y una adecuada justificación de los conceptos empleados, y realizar las operaciones matemáticas con rigor y sin errores graves.
En general, la asistencia a las clases y prácticas y la utilización de las tutorías son actividades fundamentales para el correcto seguimiento de la asignatura.
RECOMENDACIONES PARA LA RECUPERACIÓN.
Es fundamental el proceso de revisión de los exámenes no superados para afrontar con éxito la recuperación de estos: la revisión de los errores o dificultades encontrados en un examen permite subsanarlos de forma eficaz para la recuperación de cada parte de la materia.
Además de las tutorías durante el curso y de la atención continuada de forma on-line, se diseñarán una serie de tutorías colectivas e individuales una vez finalizado el periodo lectivo, con el objeto de apoyar el trabajo autónomo de los estudiantes de cara a la recuperación.


