FUNDAMENTOS DE MATEMÁTICAS II
DOBLE TITULACIÓN ING. INFORM. SISTEMAS INFORMACIÓN/GR. INFORMA. Y DOCUMENT.
Curso 2025/2026
1. Datos de la asignatura
(Fecha última modificación: 16-05-25 13:00)- Código
- 105902
- Plan
- ECTS
- 6
- Carácter
- Curso
- 1
- Periodicidad
- Primer Semestre
- Idioma
- ESPAÑOL
- Área
- GEOMETRÍA Y TOPOLOGÍA
- Departamento
- Matemáticas
- Plataforma Virtual
Datos del profesorado
- Profesor/Profesora
- Luis Alberto García Casado
- Grupo/s
- 1
- Centro
- Fac. Ciencias
- Departamento
- Matemáticas
- Área
- Geometría y Topología
- Despacho
- Edificio de La Merced, M2319 (primera planta) / Despacho 224. Edificio Administrativo
- Horario de tutorías
- Concertar cita lagc@usal.es
Lunes: 17:00 a 20:00
Miércoles: 17:00 a 20:00
Despacho 224. Edificio Administrativo
- URL Web
- http://mat.usal.es
- lagc@usal.es
- Teléfono
- -
2. Recomendaciones previas
Es obligatorio (para el correcto desarrollo de la asignatura) manejar con soltura y sin calculadora (u otro dispositivo) los siguientes contenidos algebraicos:
- Operaciones básicas matriciales
- Cálculo de determinantes de matrices cuadradas de orden hasta 4
- Cálculo de la inversa de una matriz cuadrada de orden hasta 4
- Resolución de sistemas de ecuaciones lineales con hasta 4 incógnitas.
La ausencia de dichos conocimientos previos puede dificultar el entendimiento y comprensión de los contenidos de la materia y las competencias a adquirir.
3. Objetivos
Se pretende dar los elementos de álgebra imprescindibles para una formación mínima en un grado en informática como son el Álgebra lineal, la Diagonalización de endomorfismos, la Programación lineal y el Cálculo numérico para la resolución de Sistemas de ecuaciones, que permita al alumnado tener una comprensión superior de muchas cuestiones de las que se tratan en informática, así como facilitar desde esa posición el planteamiento y resolución de problemas de modo más ágil y sencillo.
Enseñar al alumno a estructurar los contenidos específicos de un tema de forma coherente, y que éste sea capaz de desarrollarlos y transmitirlos.
4. Competencias a adquirir | Resultados de Aprendizaje
Básicas / Generales | Conocimientos.
- Poseer y comprender los conocimientos básicos y matemáticos que se desarrollan en el Grado en Ingeniería Informática en Sistemas de Información.
- Poseer las competencias que puedan demostrarse por medio de la elaboración y defensa de argumentos y de la resolución de problemas dentro del campo de la informática.
- Saber reunir e interpretar datos matemáticos relevantes para emitir juicios que incluyan una reflexión sobre temas relevantes de índole social, científica o ética.
- Poder transmitir información, ideas, problemas y sus soluciones, de forma escrita u oral, a un público tanto especializado como no especializado.
- Haber desarrollado aquellas habilidades de aprendizaje necesarias para emprender estudios posteriores con un alto grado de autonomía
Específicas | Habilidades.
CB 01. Capacidad para la resolución de los problemas matemáticos que puedan plantearse en la ingeniería. Aptitud para aplicar los conocimientos sobre: álgebra lineal; cálculo diferencial e integral; métodos numéricos; algorítmica numérica; estadística y optimización.
Transversales | Competencias.
CT 01. Capacidad de organización, gestión y planificación del trabajo.
CT 02. Capacidad de análisis, crítica y síntesis.
CT 03. Capacidad para relacionar y gestionar diversas informaciones e integrar conocimientos e ideas.
CT 04. Capacidad para comprender y elaborar modelos abstractos a partir de aspectos particulares.
CT 05. Capacidad de toma de decisiones.
CT 06. Capacidad para adaptarse a nuevas situaciones.
CT 09. Capacidad de comunicación, tanto oral como escrita, de conocimientos, ideas, procedimientos, y resultados, en lengua nativa.
CT 10. Capacidad de integración en grupos de trabajo unidisciplinares o multidisciplinares.
5. Contenidos
Teoría.
Tema 1: Espacios Vectoriales Reales
- Espacio vectorial y subespacios vectoriales
- Combinaciones lineales. Independencia lineal.
- Suma directa de subespacios vectoriales
- Bases. Dimensión. Coordenadas. Cambio de Base
Tema 2: Diagonalización
- Aplicaciones lineales. Matriz asociada a una aplicación lineal.
- Valores y vectores propios. Polinomio característico.
- Diagonalización de una matriz por semejanza.
- Ecuaciones y sistemas de ecuaciones recurrentes de sucesiones
Tema 3: Programación Lineal
- Formulación de un problema de Programación Lineal
- Método gráfico de resolución.
- Algoritmo del Símplex matricial: Método de la M-grande con variables artificiales.
Tema 4: Cálculo Numérico de Sistemas de Ecuaciones Lineales
- Condicionamiento de un sistema de ecuaciones lineales
- Métodos directos: Método LU y Método de Cholesky
- Métodos iterativos: Método de Jacobi y Método de Gauss Seidel
6. Metodologías Docentes
Metodología general como asignatura dentro de la materia Matemáticas.
En la medida de lo posible y como apoyo docente se utilizarán nuevas tecnologías tales como el desarrollo on-line de los cursos mediante la plataforma Moodle de la Universidad (Studium). A través de ella estará disponible al estudiante el material docente que se use, así como cualquier otra información relevante para el curso.
Instrumentos de la metodología docente:
Clases de Teoría y de Problemas:
Se realizarán a través de la pizarra y del cañón retroproyector.
- En las de teoría se explicarán los contenidos indicados en el programa.
- En las de problemas se mostrará sus resoluciones, para lo cual se proporcionará previamente una colección de ejercicios adecuados a los contenidos.
Aunque en estas clases de teoría y de problemas se dirige el desarrollo del programa de contenidos también pretende ser un incentivo para el resto de las actividades.
Los seminarios tutelados:
Consistirán en sesiones semanales en las que los estudiantes podrán consultar las dudas que les hayan podido surgir al resolver problemas de la hoja de ejercicios, así como sobre los problemas resueltos por el profesor en clase.
Controles de evaluación continua:
A lo largo del semestre se podrán realizar controles consistentes en la resolución de cuestiones teóricas y/o de ejercicios similares a los vistos en las clases de problemas y en los seminarios tutelados. Dichos controles serán anunciados con suficiente antelación a través de la plataforma Studium. La duración estimada de este tipo de pruebas será inferior a 2 horas.
Tutorías Individuales:
Existe un horario de tutorías a disposición del alumnado donde podrán resolver individualmente sus dudas. A estas tutorías será también donde el estudiante podrá ser citado cuando se detecten problemas de aprendizaje.
A todas testas actividades guiadas por el profesor hay que añadir que para la asimilación de los contenidos propuestos y para la adquisición de las competencias, destrezas y habilidades exigidas, cada estudiante deberá dedicar cierto tiempo de trabajo autónomo personal, tal y como se recoge el apartado 6.1
En la plataforma Studium se pondrá a disposición del colectivo, principalmente, tanto el material docente previsto como las calificaciones de los controles.
7. Distribución de las Metodologías Docentes
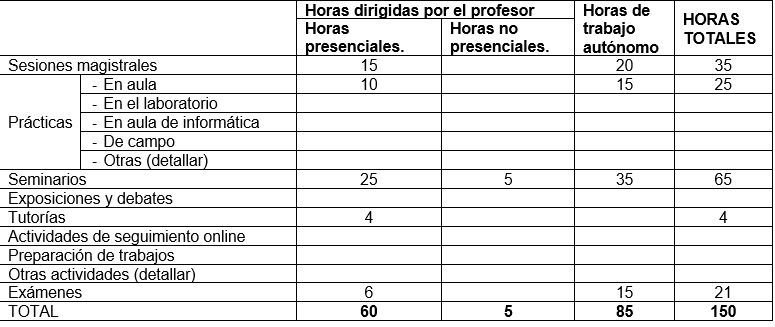
8. Recursos
Libros de consulta para el alumno.
- Álgebra lineal y geometría / Manuel Castellet, Irene Llerena, con la colaboración de Carlos Casacuberta; Ed. Reverté
- Matemática discreta y combinatoria / Ralph P. Grimaldi; Ed. Addison-Wesley.
- Linear and nonlinear programming / Luenberger, D.E. Ed. Addisson-Wesley.
- Análisis numérico / D. Kincaid, W. Cheney., Ed. Addison-Wesley
Otras referencias bibliográficas, electrónicas o cualquier otro tipo de recurso.
- Problemas resueltos de álgebra lineal: J. Arvesú, F. Marcellán y J. Sánchez; Ed. Thomson.
- Matemática discreta y sus aplicaciones: Kenneth H.Rosen. Ed. McGrawHill.
- Investigación de operaciones: Bronson, R.. Ed. Serie Schaum, McGrawHill. 1983.
- Análisis numérico: R.L. Burden, J.Douglas Faires. Ed. Paraninfo Thomson Learning.
Material proporcionado a través del Campus Virtual (Studium) de la USAL
9. Evaluación
Criterios de evaluación.
La evaluación valorará la adquisición de las competencias de carácter teórico y práctico que se comprobará tanto por actividades de evaluación continua como por una prueba escrita final.
- Las actividades de evaluación continua supondrán 40% de la nota final.
- La prueba escrita final será un 60% de la nota final Para poder superar la asignatura se requiere que la calificación obtenida en esta prueba sea al menos de 3/10
- La nota final se calculará como el máximo entre la nota del examen final (en primera o segunda convocatoria) y la nota ponderada 40% evaluación continua y 60% examen final.
Sistemas de evaluación.
Actividades de Evaluación continua:
- Pruebas escritas:
Cuando se haya impartido uno o dos temas se realizará una breve prueba escrita, en la que se pedirá la resolución de algunos ejercicios, así como de algunas preguntas de carácter teórico para valorar el grado de adquisición de las competencias específicas y transversales. La convocatoria de cada prueba prevista se indicará al alumnado al iniciar el curso.
- Pruebas tipo test:
Al acabar cada tema se podrán realizar pruebas de tipo test con preguntas teórico-prácticas para valorar el grado de adquisición de las competencias básicas. Dichas pruebas se llevarán a cabo durante los seminarios de problemas y como podrán realizarse con todo el material (no digital) que el alumnado disponga, la convocatoria de cada prueba se indicará al alumnado con una antelación de, al menos, una semana.
La media aritmética de los dos tipos de pruebas realizadas formará el 40% de la calificación final.
Prueba escrita final:
Se realizará en la fecha prevista en la planificación docente de la EPS de Zamora y tendrá una duración inferior a 3 horas. Constará de una parte teórica (30%) y de una parte práctica (70%) y será necesario superar una calificación de 3 (sobre 10) para poder hacer la media ponderada con la evaluación continua.
La nota final se calculará como el máximo entre la nota de la prueba escrita final y la nota ponderada 40% evaluación continua y 60% prueba escrita final
Calificación final de “NO PRESENTADO”:
Se asignará cuando se cumpla alguna de las condiciones siguientes:
- La no realización de más de la mitad de las pruebas de evaluación continua
- La no realización de la prueba escrita final.
- La realización de la prueba escrita final con una calificación menor o igual que 1
Recomendaciones para la evaluación.
La evaluación de las competencias de esta materia se basará principalmente en el trabajo continuado, controlado periódicamente con diferentes instrumentos de evaluación junto con una prueba escrita final.
Para la adquisición, de forma satisfactoria, de las competencias previstas en esta materia se recomienda y se tendrá en cuenta la asistencia y participación en todas las actividades programadas.
- La evaluación continua se debe interpretar como un indicador de los objetivos y destrezas que el estudiante va alcanzando. Así pues, cuando a través de esta evaluación continua se aprecien carencias en el aprendizaje se recomienda al estudiante que utilice las tutorías.
- En las tutorías, además de resolver individualmente sus dudas sobre cualquier aspecto de la asignatura, se podrán analizar las dificultades en la adquisición de competencias y, en su caso, proponer un programa de actividades ajustado a las necesidades del estudiante.
Aquellos estudiantes que mediante este sistema de evaluación no superen la asignatura tendrán la posibilidad de ser revaluados en una segunda convocatoria:
Se realizará un examen de recuperación de características similares a la prueba escrita final de la primera convocatoria (teoría 30% y problemas 70%). Y también será necesario superar una calificación de 3 (sobre 10) para poder hacer media ponderada con la evaluación continua.
Al igual que en la convocatoria ordinaria, la nota final se calculará como el máximo entre la nota del examen de recuperación y la nota ponderada 40% evaluación continua y 60% examen de recuperación.


